OBJETIVO
Con la elaboración de éste blog, acerca de la segunda unidad del curso de “Análisis de Circuitos Eléctricos de CD” cursada en 4to semestre, la cual habla del Análisis de circuitos por teoremas, se pretende:
- Reforzar el conocimiento sobre los teoremas de Norton, Thevenin, Máxima transferencia de potencia, superposición, que anteriormente hemos visto en clase.
- Transmitir la información de tal manera que el lector razone y comprenda que es lo que establece cada teorema, cuando se puede aplicar la solución de dicho teorema, la aplicación de las fórmulas dependiendo del teorema que se esté viendo, y solución de problemas por medio de cada uno de ellos.
2.1 PROPIEDAD DE LA LINEALIDAD
La linealidad es la propiedad de un elemento que describe una relación lineal entre causa y efecto. Aunque tal propiedad se aplica a muchos elementos de circuitos, en este capítulo se limitará su aplicación a resistores. Esta característica es una combinación de la propiedad de homogeneidad (escalamiento) y la propiedad aditiva. La propiedad de homogeneidad establece que si la entrada (también llamada excitación) se multiplica por una constante, la salida (también llamada respuesta) se multiplica por la misma constante. En el caso de un resistor, por ejemplo, la ley de Ohm relaciona la entrada i con la salida v,
Si la corriente se incrementa por una constante k, la tensión se incrementa en consecuencia por k; esto es,
La propiedad aditiva establece que la respuesta a una suma de entradas es la suma de las respuestas a cada entrada aplicada por separado. Con base en la relación tensión-corriente de un resistor, si
entonces la aplicación de (i1 + i2) da como resultado
En general, un circuito es lineal si es tanto aditivo como homogéneo. Un circuito lineal consta únicamente de elementos lineales, fuentes lineales dependientes y fuentes lineales independientes.
Un circuito lineal es aquel cuya salida se relaciona linealmente con (o es directamente proporcional a) su entrada.
Este circuito lineal no tiene dentro de él fuentes independientes. Es excitado por una fuente de tensión Vs, la cual sirve como entrada. El circuito termina con una carga R. Puede tomarse la corriente i a través de R como salida. Supóngase que Vs = 10 V da i = 2 A. De acuerdo con el principio de linealidad, Vs = 1 V dará en i = 0.2 A. Por la misma razón, i =1 mA tiene que deberse a Vs = 5 mV.
EJEMPLO:
2.2 TRANSFORMACIÓN DE FUENTES
La transformación de fuentes es otra herramienta para simplificar circuitos. Para estas herramientas es básico el concepto de equivalencia. Recuérdese que un circuito equivalente es aquel cuyas características de v-i son idénticas a las del circuito original. en análisis de circuitos es útil poder sustituir una fuente de tensión en serie con un resistor por una fuente de corriente en paralelo con una resistencia o viceversa, como se muestra en la siguiente figura 4.15. Cualquier sustitución se conoce como transformación de fuente.
Una transformación de fuentes es el proceso de reemplazar una fuente de tensión Vs en serie con un resistor R por una fuente de corriente Is en paralelo con un resistor R o viceversa.
Los dos circuitos de la figura 4.15 son equivalentes, en tanto tengan la misma relación tensión-corriente en las terminales a-b. Es fácil demostrar que en efecto son equivalentes. Si las fuentes se apagan, la resistencia equivalente en las terminales a-b en ambos circuitos es R. Asimismo, cuando las terminales a-b están en cortocircuito, la corriente correspondiente que fluye de A a B es Isc = Vs/R en el circuito de la izquierda e Isc = is en el de la derecha. Así, Vs/R = is para que ambos circuitos sean equivalentes. En consecuencia, la transformación de fuente requiere que
La transformación de fuentes también se aplica a fuentes dependientes, siempre y cuando se maneje con cuidado la variable dependiente. Como se muestra en la figura 4.16, una fuente de tensión dependiente en serie con un resistor puede transformarse en una fuente de corriente dependiente en paralelo con el resistor o viceversa.
Una transformación de fuente no afecta a la parte restante del circuito. Cuando es aplicable, la transformación de fuentes es una herramienta eficaz que permite manipulaciones de circuitos para facilitar su análisis. No obstante, se deben tener en cuenta los siguientes puntos al tratar con la transformación de fuentes.
- Como se advierte en la figura 4.15 (o 4.16), la flecha de la fuente de corriente apunta hacia la terminal positiva de la fuente de tensión.
- La transformación de fuente no es posible cuando R = 0, el cual es el caso de una fuente de tensión ideal. Sin embargo, en una fuente de tensión real no ideal, R ≠ 0. De igual forma, una fuente de corriente ideal con R = ∞ no puede reemplazarse por una fuente de tensión finita.
EJEMPLO:
2.2 TRANSFORMACIÓN DE FUENTES
La transformación de fuentes es otra herramienta para simplificar circuitos. Para estas herramientas es básico el concepto de equivalencia. Recuérdese que un circuito equivalente es aquel cuyas características de v-i son idénticas a las del circuito original. en análisis de circuitos es útil poder sustituir una fuente de tensión en serie con un resistor por una fuente de corriente en paralelo con una resistencia o viceversa, como se muestra en la siguiente figura 4.15. Cualquier sustitución se conoce como transformación de fuente.
Una transformación de fuentes es el proceso de reemplazar una fuente de tensión Vs en serie con un resistor R por una fuente de corriente Is en paralelo con un resistor R o viceversa.
Los dos circuitos de la figura 4.15 son equivalentes, en tanto tengan la misma relación tensión-corriente en las terminales a-b. Es fácil demostrar que en efecto son equivalentes. Si las fuentes se apagan, la resistencia equivalente en las terminales a-b en ambos circuitos es R. Asimismo, cuando las terminales a-b están en cortocircuito, la corriente correspondiente que fluye de A a B es Isc = Vs/R en el circuito de la izquierda e Isc = is en el de la derecha. Así, Vs/R = is para que ambos circuitos sean equivalentes. En consecuencia, la transformación de fuente requiere que
La transformación de fuentes también se aplica a fuentes dependientes, siempre y cuando se maneje con cuidado la variable dependiente. Como se muestra en la figura 4.16, una fuente de tensión dependiente en serie con un resistor puede transformarse en una fuente de corriente dependiente en paralelo con el resistor o viceversa.
Una transformación de fuente no afecta a la parte restante del circuito. Cuando es aplicable, la transformación de fuentes es una herramienta eficaz que permite manipulaciones de circuitos para facilitar su análisis. No obstante, se deben tener en cuenta los siguientes puntos al tratar con la transformación de fuentes.
- Como se advierte en la figura 4.15 (o 4.16), la flecha de la fuente de corriente apunta hacia la terminal positiva de la fuente de tensión.
- La transformación de fuente no es posible cuando R = 0, el cual es el caso de una fuente de tensión ideal. Sin embargo, en una fuente de tensión real no ideal, R ≠ 0. De igual forma, una fuente de corriente ideal con R = ∞ no puede reemplazarse por una fuente de tensión finita.
EJEMPLO:
2.3 TEOREMA DE SUPERPOSICIÓN
Si un circuito tiene dos o más fuentes independientes, una forma de determinar el valor de una variable específica (tensión o corriente) es aplicar el análisis nodal o de malla, como en la unidad 1. Otra es determinar la contribución de cada fuente independiente a la variable y después sumarlas. Este último método se conoce como superposición. La idea de la superposición se basa en la propiedad de la linealidad.
El principio de superposición establece que la tensión entre los extremos (o la corriente a través) de un elemento en un circuito lineal es la suma algebraica de las tensiones (o corrientes) a través de ese elemento debido a que cada fuente independiente actúa sola.
El principio de superposición ayuda a analizar un circuito lineal con más de una fuente independiente, mediante el cálculo de la contribución de cada fuente independiente por separado. Sin embargo, al aplicarlo deben tenerse en cuenta dos cosas:
- Las fuentes independientes se consideran una a la vez mientras todas las demás fuentes independientes están apagadas. Esto implica que cada fuente de tensión se reemplaza por 0 V (o cortocircuito) y cada fuente de corriente por 0 A (o circuito abierto). De este modo se obtiene un circuito más simple y manejable.
- Las fuentes dependientes se dejan intactas, porque las controlan variables de circuitos.
Pasos para aplicar el principio de superposición:
- Apague todas las fuentes independientes, excepto una. Determine la salida (tensión o corriente) debida a esa fuente activa.
- Repita el paso 1 en cada una de las demás fuentes independientes.
- Halle la contribución total sumando algebraicamente todas las contribuciones debidas a las fuentes independientes.
El análisis de un circuito aplicando la superposición tiene una gran desventaja: muy probablemente puede implicar más trabajo. Si el circuito tiene tres fuentes independientes, quizá deban analizarse tres circuitos más simples, cada uno de los cuales proporciona la contribución debida a la respectiva fuente individual. Sin embargo, la superposición ayuda a reducir un circuito complejo en circuitos más simples mediante el reemplazo de fuentes de tensión por cortocircuitos y de fuentes de corriente por circuitos abiertos.
EJEMPLO:
2.4 TEOREMA DE THEVENIN
El teorema de Thevenin establece que un circuito lineal de dos terminales puede reemplazarse por un circuito equivalente que consta de una fuente de tensión VTh en serie con un resistor RTh, donde VTh es la tensión de circuito abierto en las terminales y RTh es la entrada o resistencia equivalente en las terminales cuando las fuentes independientes se apagan.
De acuerdo con el teorema de Thevenin, el circuito lineal de la figura 4.23a) puede reemplazarse por el de la figura 4.23b). (La carga en la figura 4.23 puede ser un solo resistor u otro circuito.) El circuito a la izquierda de las terminales a-b en la figura 4.23b) se conoce como circuito equivalente de Thevenin y fue desarrollado en 1883 por el ingeniero de telégrafos francés M. Leon Thevenin (1857-1926).
Se dice que dos circuitos son equivalentes si tienen la misma relación tensión-corriente en sus terminales. Indáguese qué vuelve equivalentes a los circuitos de la figura 4.23. Si las terminales a-b están en circuito abierto (mediante la eliminación de la carga), ninguna corriente fluye, así que la tensión de circuito abierto entre las terminales a-b de la figura 4.23a) debe ser igual a la fuente de tensión VTh de la figura 4.23b), ya que ambos circuitos son equivalentes. Así, VTh es la tensión de circuito abierto entre las terminales, como se indica en la figura 4.24a); es decir,
De nueva cuenta, con la carga desconectada y las terminales a-b en circuito abierto, se apagan todas las fuentes independientes. La resistencia de entrada (o resistencia equivalente) del circuito apagado en las terminales a-b de la figura 4.23a) debe ser igual a RTh en la figura 4.23b), porque ambos circuitos son equivalentes. Así, RTh es la resistencia de entrada, en las terminales cuando las fuentes independientes se apagan, como se muestra en la figura 4.24b); es decir,
Para aplicar esta idea en el cálculo de la resistencia de Thevenin RTh se deben considerar dos casos.
- CASO 1 Si la red no tiene fuentes dependientes, se apagan todas las fuentes independientes. RTh es la resistencia de entrada que aparece entre las terminales a y b, como se advierte en la figura 4.24b).
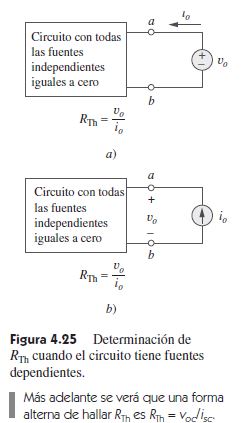
- CASO 2 Si la red tiene fuentes dependientes, se apagan todas las fuentes independientes. Como en el caso de la superposición, las fuentes dependientes no se desactivan, porque son controladas por las variables del circuito. Se aplica una fuente de tensión Vo en las terminales a y b y se determina la corriente resultante Io. Así, RTh = Vo /Io, como se señala en la figura 4.25a)
Como ya se mencionó, un circuito lineal con una carga variable puede reemplazarse por el equivalente de Thevenin, exclusivo para la carga. La red equivalente se comporta externamente de la misma manera que el circuito original. Considérese un circuito lineal que termina con una carga RL, como se advierte en la figura 4.26a). La corriente IL a través de la carga y la tensión VL en sus terminales se determinan con facilidad una vez que se obtiene el equivalente de Thevenin del circuito en las terminales de la carga, como se muestra en la figura 4.26b). Con base en esta última figura, se obtiene
EJEMPLO:
2.5 TEOREMA DE NORTON
El teorema de Norton establece que un circuito lineal de dos terminales puede reemplazarse por un circuito equivalente que consta de una fuente de corriente IN en paralelo con un resistor RN, donde IN es la corriente de cortocircuito a través de las terminales y RN es la resistencia de entrada o resistencia equivalente en las terminales cuando las fuentes independientes están desactivadas.
Así, el circuito de la figura 4.37a) puede reemplazarse por el de la figura 4.37b). La demostración del teorema de Norton se dará en la siguiente sección. Por ahora interesa principalmente cómo obtener RN e IN. RN se halla de la misma manera que RTh. De hecho, por lo que ya se sabe sobre la transformación de fuente, las resistencias de Thevenin y de Norton son iguales; es decir,
Para encontrar la corriente de Norton IN, se determina la corriente de cortocircuito que fluye de la terminal a a la b en los dos circuitos de la figura 4.37. Es evidente que la corriente de cortocircuito de la figura 4.37b) es IN. Ésta debe ser igual a la corriente de cortocircuito de la terminal a a la b de la figura 4.37a), ya que ambos circuitos son equivalentes. Así,
como se indica en la figura 4.38. Las fuentes dependientes e independientes se tratan igual que en el teorema de Thevenin. Obsérvese la estrecha relación entre los teoremas de Norton y de Thevenin: RN =RTh como en la ecuación (4.9)
Puesto que VTh, IN y RTh se relacionan de acuerdo con la ecuación (4.11), para determinar el circuito equivalente de Thevenin o de Norton se requiere hallar:
- La tensión de circuito abierto Voc entre las terminales a y b.
- La corriente de cortocircuito Isc por las terminales a y b.
- La resistencia equivalente o de entrada Ren en las terminales a y b cuando todas las fuentes independientes están apagadas.
Se pueden calcular dos de las tres siguiendo el método que implique el menor esfuerzo y emplearlas para obtener la tercera aplicando la ley de Ohm.
EJEMPLO:
2.6 TEOREMA DE MÁXIMA TRANSFERENCIA DE POTENCIA
El equivalente de Thevenin es útil para hallar la máxima potencia que un circuito lineal puede suministrar a una carga. Supóngase que se puede ajustar la resistencia de carga RL. Si el circuito entero se reemplaza por su equivalente de Thevenin exceptuando la carga, como se muestra en la figura 4.48, la potencia suministrada a la carga es
En un circuito dado, VTh y RTh son fijos. Al variar la resistencia de carga RL, la potencia suministrada a la carga varía como se indica gráficamente en la figura 4.49. En esta figura se advierte que la potencia es mínima para valores pequeños o grandes de RL, pero máxima respecto de algún valor de RL entre 0 y ∞. Ahora se debe demostrar que esta máxima potencia ocurre cuando RL es igual a RTh. Esto se conoce como teorema de máxima potencia.
La máxima potencia se transfiere a la carga cuando la resistencia de la carga es igual a la resistencia de Thevenin vista desde la carga (RL = RTh).
Para comprobar el teorema de la máxima transferencia de potencia, se deriva p en la ecuación (4.21) respecto a RL y se fija el resultado en cero. De ello se obtiene
La máxima potencia transferida se obtiene sustituyendo la ecuación (4.23) en la ecuación (4.21), de lo que resulta
La ecuación (4.24) sólo se aplica cuando RL = RTh. Cuando RL ≠ RTh, la potencia suministrada a la carga se calcula mediante la ecuación (4.21).
EJEMPLO:
2.7 APLICACIÓN DE SOFTWARE
Usando el programa EveryCircuit:
https://www.youtube.com/watch?v=dkTFqTiB-_U&t=13s
Usando Cocodrile Clips:
https://www.youtube.com/watch?v=2l0iMMWOu0I&t=96s
Usando Proteus Básico:
https://www.youtube.com/watch?v=dkTFqTiB-_U&t=13s
Usando Cocodrile Clips:
https://www.youtube.com/watch?v=2l0iMMWOu0I&t=96s
Usando Proteus Básico:
BIBLIOGRAFÍA:
Alexander, C. K. (2006). Fundamentos de circuitos electricos. Mexico, D.F: McGraw-Hill.
Floyd, T. L. (2007). Principios de circuitos electricos. Mexico: PEARSON EDUCACION.
Irwin, J. D. (1997). Analisis basicos de circuitos en ingenieria. Edo. de Mexico: Prentice-Hall.
Nilsson, J. W. (2005). Circuitos electricos. Madrid: PEARSON EDUCACION.
Robbins, A. H. (2008). Analisis de circuitos: teoria y practica. Mexico, D.F: Cengage Learning.
NOTA: Para ver mas ejercicios y complementar los conocimientos adquiridos, dar click en el vinculo en el nombre de los libros de las bibliografías
Blog realizado por:
Blog realizado por:
Daniel Llanos
Antonio Guerrero
Fernando Méndez






















No comments:
Post a Comment